import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2

# Plot for n=1 parameter
def plot_chi2_n1():
    x = np.linspace(0, 6, 1000)
    chi2_1d_pdf = chi2.pdf(x, df=1)
    
    plt.figure(figsize=(7, 7))
    plt.plot(x, chi2_1d_pdf, 'b-', label='χ² Distribution (df=1)', linewidth=2)
    
#    conf_region_x = x[x <= 4.00]
    conf_region_x = x[x <= 4.00]
    conf_region_y = chi2.pdf(conf_region_x, df=1)
#    plt.fill_between(conf_region_x, conf_region_y, alpha=0.3, color='blue',
#                     label=f'{chi2.cdf(1.00, df=1):.2%} Confidence Region')
    
    plt.fill_between(conf_region_x, conf_region_y, alpha=0.3, color='blue',
                     label=f'{chi2.cdf(4.00, df=1):.2%} Confidence Region')

    plt.axvline(x=4.00, color='red', linestyle='--', label='Δχ² = 1.00')
#    plt.title('Chi-square Distribution for n=1 Parameter\n'
#              f'Δχ² ≈ 1.00 for 68.27% Confidence Level',
#              fontsize=12, pad=15)
    plt.title('Chi-square Distribution for n=1 Parameter\n'
              f'Δχ² ≈ 4.00 for 95.45% Confidence Level',
              fontsize=12, pad=15)
    plt.xlabel('χ² Value')
    plt.ylabel('Probability Density')
    plt.grid(True, alpha=0.3)
    plt.legend(fontsize=10)
    plt.show()

# Plot for n=2 parameters
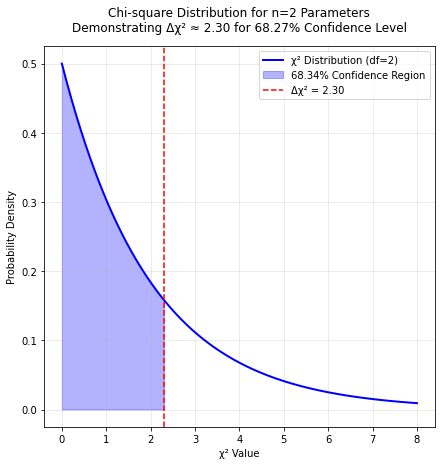
def plot_chi2_n2():
    x = np.linspace(0, 8, 1000)
    chi2_2d_pdf = chi2.pdf(x, df=2)
    
    plt.figure(figsize=(7, 7))
    plt.plot(x, chi2_2d_pdf, 'b-', label='χ² Distribution (df=2)', linewidth=2)
    
    conf_region_x = x[x <= 2.30]
    conf_region_y = chi2.pdf(conf_region_x, df=2)
    plt.fill_between(conf_region_x, conf_region_y, alpha=0.3, color='blue',
                     label=f'{chi2.cdf(2.30, df=2):.2%} Confidence Region')
    
    plt.axvline(x=2.30, color='red', linestyle='--', label='Δχ² = 2.30')
    plt.title('Chi-square Distribution for n=2 Parameters\n'
              f'Demonstrating Δχ² ≈ 2.30 for 68.27% Confidence Level',
              fontsize=12, pad=15)
    plt.xlabel('χ² Value')
    plt.ylabel('Probability Density')
    plt.grid(True, alpha=0.3)
    plt.legend(fontsize=10)
    plt.show()

plot_chi2_n1()

plot_chi2_n2()